- 유머가 아닌 펌글, 영상 등 가볍게 볼 수 있는 글들도 게시가 가능합니다.
- 여러 회원들이 함께 사용하기 위해 각 회원당 하루 5개로 횟수제한이 있습니다.
- 특정인 비방성 자료는 삼가주십시오.
| Date | 16/10/05 07:02:38 |
| Name | 김치찌개 |
| File #1 | 1.jpg (14.1 KB), Download : 62 |
| Subject | 초등학교 기출.jpg |
|
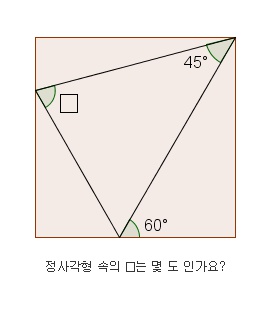
초등학교 기출 0
이 게시판에 등록된 김치찌개님의 최근 게시물
|
|
음... 대애충 쓰자면. 일단 저기서 x가 특정지어지려면 아무 직사각형이면 안됩니다. 주어진 조건 (45도 및 60도) 내에서 사각형의 가로 세로 길이가 변할 경우 x가 변할 수 있겠지요. 즉 정사각형임을 무조건 이용해야만 풀 수 있어요.
삼각형 내각의 합이 180도 이용해서 아래쪽에 60도 주어졌죠? 그럼 우상단에 45도 아래쪽이 30도가 되요. 45도 위쪽에는 90-45-30=15... 식으로 바로 각도 나오는 애들은 다 써두고 나서, 정사각형의 방향으로 보조선을 / 그은 그 선 위 아래로 45도니까(정사각형이어야만 나올 수 있는 각도) 이래저래 각도 쓰고 더하고 뺴면 답 나올거에요.
삼각형 내각의 합이 180도 이용해서 아래쪽에 60도 주어졌죠? 그럼 우상단에 45도 아래쪽이 30도가 되요. 45도 위쪽에는 90-45-30=15... 식으로 바로 각도 나오는 애들은 다 써두고 나서, 정사각형의 방향으로 보조선을 / 그은 그 선 위 아래로 45도니까(정사각형이어야만 나올 수 있는 각도) 이래저래 각도 쓰고 더하고 뺴면 답 나올거에요.
피타고라스 정리 -> 삼각함수 / 연립방정식 모두 중학교 수학 교과과정입니다.
사실 외각내각이니 내각합이 pi()/2니 엇각이니 동위각이니 하는 평면도형에서의 개념과 응용문제들도 00년대와 달리 현재는 중학교 수학 교과과정인데
현재 초등학교 수학 교과과정에도 예각이니 둔각이니 하며 평면도형에 대해 다루고는 있으니(이 삼각형이 예각삼각형이다! 정도만 배웁니다만) 좀 양보해 줘서 초등학교 과정이라 인정할 수 있다고 하면
Cogito님이 말씀하신 것처럼 평행선이나 대각선, 맞붙여 그릴 수 있는 다른 정사각형 등의 보조선... 더 보기
사실 외각내각이니 내각합이 pi()/2니 엇각이니 동위각이니 하는 평면도형에서의 개념과 응용문제들도 00년대와 달리 현재는 중학교 수학 교과과정인데
현재 초등학교 수학 교과과정에도 예각이니 둔각이니 하며 평면도형에 대해 다루고는 있으니(이 삼각형이 예각삼각형이다! 정도만 배웁니다만) 좀 양보해 줘서 초등학교 과정이라 인정할 수 있다고 하면
Cogito님이 말씀하신 것처럼 평행선이나 대각선, 맞붙여 그릴 수 있는 다른 정사각형 등의 보조선... 더 보기
피타고라스 정리 -> 삼각함수 / 연립방정식 모두 중학교 수학 교과과정입니다.
사실 외각내각이니 내각합이 pi()/2니 엇각이니 동위각이니 하는 평면도형에서의 개념과 응용문제들도 00년대와 달리 현재는 중학교 수학 교과과정인데
현재 초등학교 수학 교과과정에도 예각이니 둔각이니 하며 평면도형에 대해 다루고는 있으니(이 삼각형이 예각삼각형이다! 정도만 배웁니다만) 좀 양보해 줘서 초등학교 과정이라 인정할 수 있다고 하면
Cogito님이 말씀하신 것처럼 평행선이나 대각선, 맞붙여 그릴 수 있는 다른 정사각형 등의 보조선을 이용해서 푸는 것이 출제자(글 게시자)가 말한 "초등학교 기출"의 의도에 부합하는 방법일 겁니다.
마침 elanor님이 구해주신 답이 특수각(이고 원래 문제에서 주어진 조건 중 같은 값인 각도도 있으니) 보조선, 합동이나 닮음 등을 어떻게 버무리면 답에 끼워맞춘 "초등학교 기출"수준의 풀이과정을 만들어 낼 수 있을 것 같기도 하고 안될 것 같기도 한데...
논문쓰기 싫어서 하는 헛소리는 여기까지만 하겠습니다 ㅠㅠ
사실 외각내각이니 내각합이 pi()/2니 엇각이니 동위각이니 하는 평면도형에서의 개념과 응용문제들도 00년대와 달리 현재는 중학교 수학 교과과정인데
현재 초등학교 수학 교과과정에도 예각이니 둔각이니 하며 평면도형에 대해 다루고는 있으니(이 삼각형이 예각삼각형이다! 정도만 배웁니다만) 좀 양보해 줘서 초등학교 과정이라 인정할 수 있다고 하면
Cogito님이 말씀하신 것처럼 평행선이나 대각선, 맞붙여 그릴 수 있는 다른 정사각형 등의 보조선을 이용해서 푸는 것이 출제자(글 게시자)가 말한 "초등학교 기출"의 의도에 부합하는 방법일 겁니다.
마침 elanor님이 구해주신 답이 특수각(이고 원래 문제에서 주어진 조건 중 같은 값인 각도도 있으니) 보조선, 합동이나 닮음 등을 어떻게 버무리면 답에 끼워맞춘 "초등학교 기출"수준의 풀이과정을 만들어 낼 수 있을 것 같기도 하고 안될 것 같기도 한데...
논문쓰기 싫어서 하는 헛소리는 여기까지만 하겠습니다 ㅠㅠ
삼각함수 안 쓰고 하려니까 무척 어렵네요.
1. 정사각형의 좌하-우상으로 대각선 하나 긋고, 오른쪽 아래 모서리에서 왼쪽 위로 직선 하나 긋습니다. 각도는 바닥과 60도 되게요. 여러 각도를 구하다보면 양 변이 75도인 이등변삼각형을 발견할 수 있습니다. 왼쪽 사선과 60도로 새로 그은 선(이등변 삼각형의 밑변)이 수평인 것 같이 보이기 때문에, 이를 증명해내면 답인 75도를 쉽게 구할 수 있습니다.
2. 문제는 두 선분이 평행이라는 것을 증명하는 게 꽤 어렵더군요. 선 잘 긋는게 어려워서요. 왼쪽 아래에서 새로 그은 선... 더 보기
1. 정사각형의 좌하-우상으로 대각선 하나 긋고, 오른쪽 아래 모서리에서 왼쪽 위로 직선 하나 긋습니다. 각도는 바닥과 60도 되게요. 여러 각도를 구하다보면 양 변이 75도인 이등변삼각형을 발견할 수 있습니다. 왼쪽 사선과 60도로 새로 그은 선(이등변 삼각형의 밑변)이 수평인 것 같이 보이기 때문에, 이를 증명해내면 답인 75도를 쉽게 구할 수 있습니다.
2. 문제는 두 선분이 평행이라는 것을 증명하는 게 꽤 어렵더군요. 선 잘 긋는게 어려워서요. 왼쪽 아래에서 새로 그은 선... 더 보기
삼각함수 안 쓰고 하려니까 무척 어렵네요.
1. 정사각형의 좌하-우상으로 대각선 하나 긋고, 오른쪽 아래 모서리에서 왼쪽 위로 직선 하나 긋습니다. 각도는 바닥과 60도 되게요. 여러 각도를 구하다보면 양 변이 75도인 이등변삼각형을 발견할 수 있습니다. 왼쪽 사선과 60도로 새로 그은 선(이등변 삼각형의 밑변)이 수평인 것 같이 보이기 때문에, 이를 증명해내면 답인 75도를 쉽게 구할 수 있습니다.
2. 문제는 두 선분이 평행이라는 것을 증명하는 게 꽤 어렵더군요. 선 잘 긋는게 어려워서요. 왼쪽 아래에서 새로 그은 선 덕에 새로운 교점이 생겼을 겁니다. 이 점을 기준으로 정사각형을 위아래로 이등분하는 선을 긋습니다. 아랫변 가운데 근처에 선분이 3개 모인 점에서 직각으로 선을 긋습니다. 중앙 우측 교점에서 바로 전에 그은 선을 기준으로 왼쪽 위 30도 방향으로 선을 또 긋습니다. 정사각형의 위쪽 변을 왼쪽으로 연장합니다. 윗변에 새로 생긴 교점에서 왼쪽 아래 60도 방향으로 선분을 또 긋습니다. 구하는 각 x에서 정사각형 위쪽 변이 연장해 다른 선이랑 맞닿은 곳으로 선을 긋습니다. 이렇게 하면 커다란 직각삼각형 두 개와 정삼각형처럼 보이는 도형 두 개를 추가로 만들 수 있습니다.
3. 선 긋는 게 어렵지 이제는 합동 놀이 하시면 됩니다. 일단 새로 생긴 직각삼각형들 중에 큰 것 두 개가 합동임을 증명합니다. 그리고 그 안에 있는 둔각이등변삼각형이 SSS 합동임을 증명합니다. 그리고 왼쪽 위의 정삼각형 같은 도형이 정삼각형임을 증명하고, 아래도 마찬가지입니다. 이 두 도형이 정삼각형임을 증명하면 1번의 수평이 자동 증명되기 때문에 구하는 각은 75도입니다.
한줄요약. 파타고라스에게 하루 세번씩 절합시다.
1. 정사각형의 좌하-우상으로 대각선 하나 긋고, 오른쪽 아래 모서리에서 왼쪽 위로 직선 하나 긋습니다. 각도는 바닥과 60도 되게요. 여러 각도를 구하다보면 양 변이 75도인 이등변삼각형을 발견할 수 있습니다. 왼쪽 사선과 60도로 새로 그은 선(이등변 삼각형의 밑변)이 수평인 것 같이 보이기 때문에, 이를 증명해내면 답인 75도를 쉽게 구할 수 있습니다.
2. 문제는 두 선분이 평행이라는 것을 증명하는 게 꽤 어렵더군요. 선 잘 긋는게 어려워서요. 왼쪽 아래에서 새로 그은 선 덕에 새로운 교점이 생겼을 겁니다. 이 점을 기준으로 정사각형을 위아래로 이등분하는 선을 긋습니다. 아랫변 가운데 근처에 선분이 3개 모인 점에서 직각으로 선을 긋습니다. 중앙 우측 교점에서 바로 전에 그은 선을 기준으로 왼쪽 위 30도 방향으로 선을 또 긋습니다. 정사각형의 위쪽 변을 왼쪽으로 연장합니다. 윗변에 새로 생긴 교점에서 왼쪽 아래 60도 방향으로 선분을 또 긋습니다. 구하는 각 x에서 정사각형 위쪽 변이 연장해 다른 선이랑 맞닿은 곳으로 선을 긋습니다. 이렇게 하면 커다란 직각삼각형 두 개와 정삼각형처럼 보이는 도형 두 개를 추가로 만들 수 있습니다.
3. 선 긋는 게 어렵지 이제는 합동 놀이 하시면 됩니다. 일단 새로 생긴 직각삼각형들 중에 큰 것 두 개가 합동임을 증명합니다. 그리고 그 안에 있는 둔각이등변삼각형이 SSS 합동임을 증명합니다. 그리고 왼쪽 위의 정삼각형 같은 도형이 정삼각형임을 증명하고, 아래도 마찬가지입니다. 이 두 도형이 정삼각형임을 증명하면 1번의 수평이 자동 증명되기 때문에 구하는 각은 75도입니다.
한줄요약. 파타고라스에게 하루 세번씩 절합시다.
| 목록 |
|