- 다양한 주제에 대해 자유롭게 글을 작성하는 게시판입니다.
| Date | 18/10/11 05:03:35 |
| Name | Sophie |
| Link #1 | https://en.wikipedia.org/wiki/Bayesian_inference |
| Link #2 | http://pi.math.cornell.edu/~mec/2008-2009/TianyiZheng/Bayes.html |
| Subject | [확률론] 당신은 암에 걸리지 않았다 - 의사들도 잘 모르는 사실 |
|
의료넷에서 일단 제목으로 어그로 좀 끌었습니다. 제가 짧게 쓸 글은 베이지안 추론에 관한 글입니다. 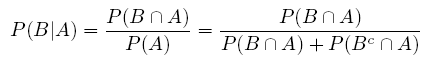 한번 쯤을 배웠을법한 베이즈 정리에서 출발합니다. 질문: 40-50세 여성중 대략 1%정도는 유방암에 걸린다. 유방암에 걸린 여성은 90%의 확률로 유방촬영술후 양성판정을 받게되고 정상 여성도 10퍼센트의 양성판정 확률이 있다. 한 여성이 유방촬영술로 양성판정을 받았을때 유방암에 걸렸을 확률은? 95명의 의사에게 이 질문을 했을때 평균을 내보면 75%라고 합니다. 보기엔 상식적인 확률로 보입니다. 베이지안 추론으로 그게 맞는지 확인해봅시다. A를 유방촬영술 양성판정 B를 유방암이 있음 로 정의하고 이 질문은 P(B|A)를 찾는 조건부 확률 문제가 됩니다. P(B|A)를 베이즈 추론으로 찾기 위해선 확률 3개가 필요합니다. 1. P(B) 2. P(A|B) 3. P(A) 그럼 문제를 풀어봅시다. 1. [40-50세 여성중 대략 1%정도는 유방암에 걸린다] -> P(B) = 0.01 2. [유방암에 걸린 여성은 90%의 확률로 유방촬영술후 양성판정] -> P(A | B) = 0.9 3. [정상 여성도 10퍼센트의 양성판정 확률] -> P(A | not B) = 0.1 P(not B) = 1 - P(B) = 0.99 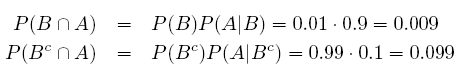 답: 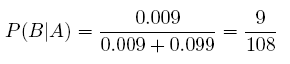 고작 8.3%에 불과합니다. 암을 정기검사같은 어떤 [사전정보 없이] 검사했을 경우 양성판정을 받았다고 해도 실제로 암이 있을 확률은 생각보다 높지 않다는거죠. 베이지안 추론에서 재밌는점은 사후확률을 사전확률로 업데이트할수 있다는 점입니다. 사후확률 P(B | A)을 사전확률 P(B) = .083 로 설정하고 문제를 다시 풀어본다면 사후확률은 45%입니다. 한번 더 반복하면 88%가 됩니다. 그럼 다시 처음으로 돌아가서 테스트의 양성판정률을 99%로 올려봅시다. P(A|B) = 0.99로 설정하고 다시 풀어본다면 베이지안 추론으로도 많이 올라가겠죠? 계산을 해보니 9.1% 밖에 되지 않습니다. 사전정보없이 한번의 테스트로 사후 확률을 높이고 싶으면 [정상 여성도 10퍼센트의 양성판정 확률]을 내려야 합니다. 동일조건으로 이 확률만 1퍼센트로 낮추고 다시 계산한다면 한번의 테스트만으로 유방암에 걸렸을 확률은 48%이 됩니다. 1줄 결론: 사전정보와 민감도와 특이도는 매우 중요하다. 10
이 게시판에 등록된 Sophie님의 최근 게시물 |
|





